Alexandre Texier

Avec un titre pareil, on pourrait croire que l’on se dirige sur l’idée d’une soi-disant forme parfaite de la typographie, aux relents de conservatisme, et bien non. On pourrait également penser qu’il va s’agir de parler d’une culture typographique vernaculaire, propre à une zone géographique et en faire un safari ? Si la chose est intéressante, puisqu’il en existe des exemples, ici, un léger pas de côté va être fait.

Tout en restant légèrement chauvins – puisqu’il s’agira surtout du cas breton – nous allons explorer des voies de création typographique à rebours du verre de cristal : des signes pensés pour refléter une histoire, un patrimoine et une culture locale. En plus, il y a une certaine actualité.

Degemer mat e Breizh

Avec son travail intitulé « La bolée de cristal », Jeanne Saliou, qui a très récemment quitté les bancs de l’ANRT, nous propose un caractère typographique embrassant pleinement la culture bretonne du point de vue du dessin de caractère. En effet, le Gwenhadu (s’il s’agit bien là du nom du caractère, chose dont je ne suis totalement sûr) propose un caractère de labeur intégrant des formes rappelant la traduction calligraphique et typographique de l’espace culturel breton. Cela passe par des formes enluminées des capitales, en forme de clin d’œil, mais aussi, et de façon plus directement palpable, de ‹ G › et de ‹ g › peu habituels pour le commun des mortels. S’ajoutent aussi deux sets stylistiques pour aller plus loin dans la coloration du texte, mais également un ensemble de ligatures et glyphes spécifiques. On trouvera évidemment le fameux ‹ Ꝃ › [K barré], signe abréviatif pour Ker pouvant signifier chez, ville, ou plus généralement un lieu. Finalement, il est assez proche de ‹ & › [esperluette], signe abréviatif pour et, sauf que lui ne s’est pas fait interdire par l’État en 1895, et ne suscite pas particulièrement de tensions, comme le suggère Yann Saliou en 1992. Le breton étant ce qu’il est, son utilisation de l’alphabet latin diffère du français. Ainsi certaines successions de lettres ont permis de proposer des ligatures très spécifiques : ‹ zh ›, ‹ gn ›, ‹ c’h › ; ou plus étonnantes pour une personne ne sachant rien (comme moi-même) du breton : ‹ vM › et ‹ gK ›, avec une minuscule avant une majuscule, oui.

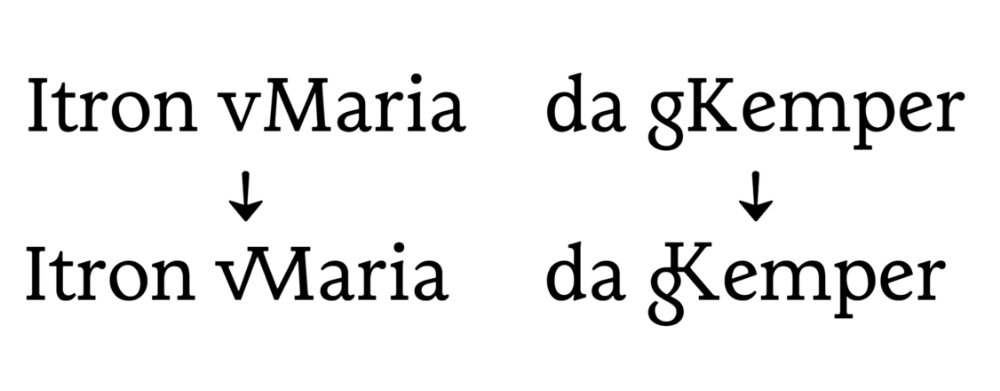
Inscrit dans des problématiques contemporaines, le caractère intègre également un ensemble de ligatures spécifiques à ce qui pourrait devenir un breton inclusif, offrant entre autres des ligatures pour ‹ re ›, ‹ vb ›, ‹ Gc’h › et ‹ c’hg ›. Il semble donc que le breton entre dans une ère contemporaine dont la typographie peut fournir à la fois une identité graphique, et répondre à des enjeux à la fois linguistiques, patrimoniaux et actuels.

Rannvro Breizh

Si le travail de cette designer est le plus récent que je connaisse, ce travail de modélisation typographique de la Bretagne n’est pas nouveau. Pour les Bretons c’est assez familier, pour les autres peut-être moins, mais nous associons déjà la région à une forme typographique : celle de sa communication officielle. Elle utilise un caractère exclusif dessiné par Xavier Dupré à partir de son caractère Spotka, le Région Bretagne, dont les terminaisons de lettres et les capitales spécifiques feront probablement surgir un ding dans votre mémoire.

Au-delà de la commande officielle, on peut évidemment citer Skritur, studio de design graphique et typographique fondé par Fañch Le Henaff, Malou Verlomme et Yoann De Roeck qui « recense, décrypte, interprète et conçoit dans le champ de la chose écrite (inscrite, calligraphique, typographique) en Bretagne particulièrement, mais plus largement les pays celtiques et dans tout lieu où se mêlent les particularismes idiomatiques et les graphies singulières ». La structure propose ainsi des caractères inspirés très directement de la culture bretonne et plus généralement celte donc, que je vous laisserai découvrir, mais également des articles sur le patrimoine graphique et typographique de la région. Pour dire la démarche jusqu’au-boutiste de la structure, rappelons que Yoan De Roeck est en ce moment même en train de mener une recherche doctorale fort à propos : « L’immatriculation des chaloupes en Bretagne (1852–1914) – Approche typographique d’un phénomène d’épigraphie vernaculaire » dirigée par Marc Smith, probablement l’épigraphe français le plus célèbre, et dont la Véridique histoire de l’arobase, publiée récemment, est un must-have pour les curieux des signes.

Nos régions ont du talent (graphique)

Le cas breton est assez significatif des possibilités offertes par la typographie dans la mise en avant d’un patrimoine culturel régional, et évidemment, il y a d’autres exemples à citer maintenant, sans toutefois prétendre à une quelconque exhaustivité.

Pour rester dans la communication publique, évoquons le travail non retenu du studio Graphéine pour un nouveau logo de Biarritz, reprenant des formes de lettres inspirées par la graphie basque, avec notamment le ‹ A › à traverse en pointe et double serif en chef.

Pour le versant typo-linguistique, citons le travail d’Agnès Brézéphin sur le Coolie, avec des ligatures pour le parler créole ; le Pitchoune de Yann Linguinou pour le parler marseillais ; le Traulha, issu du projet de diplôme de Yoann Minet qui s’intéressait quant à lui à la culture occitane ; la proposition de ligature ‹ hj › spécifique au corse de Xavier Dandoy ; et enfin le Munegascu de Bruno Bernard – basé sur l’Archivo – qui intègre des diacritiques (des accents) spécifiques au monégasque. Pour terminer avec ces exemples, n’oublions pas la fiction et le Bubunne de Fanette Mellier, pensé pour le film Jacky au royaume des filles de Riad Sattouf, où l’on constate qu’une dystopie fascho-communo-féministe (oui, je vous laisse avec ça) a bien besoin d’une forme typographique adéquate.

Entre le verre de cristal – le texte invisible – et la bolée – le texte culturellement et géographiquement ancré – l’éventail des formes typographiques est grand. Les possibilités techniques actuelles avec les sets stylistiques et les ligatures/ligatures conditionnelles facilitent ce type de créations. Il faudrait néanmoins que l’encodage typographique suive. Si c’est le cas pour le ‹ Ꝃ › et le ‹ ꝃ › depuis 2008 avec Unicode 5.1.0, qu’en est-il d’autres formes typographiques régionales, voire nationales ?

Spoiler alert : il y a encore du travail.

1. Jeanne Saliou, « La bolée de cristal – dessiner un caractère adapté à la lecture longue en breton », ANRT, 03/2025, 35 min (source)
2. Xavier Dupré, « Région Bretagne » (source)
3. Région Bretagne, « Charte graphique Région Bretagne – édition 2016 », 2016 (source PDF)
4. Yann Riou, « Le k barré d’hier à aujourd’hui », association Lambaol, 1992 (source PDF)
5. Julien Marchand, « Le k barré : la lettre interdite », Bikini, 63, 09-10/2023, p. 26-31 (source)
6. Skritur, « Our project » (source)
7. Yoan De Roeck, « L’immatriculation des chaloupes en Bretagne (1852-1914) – Approche typographique d’un phénomène d’épigraphie vernaculaire », theses.fr, depuis 2021 (source)
8. Marc H. Smith, La véridique histoire de l’arobase, « Propos », École des chartes éditions, 2024 (source)
9. Graphéine, « Projet d’identité visuelle pour la Ville de Biarritz », 06/04/2023 (source)
10. Yann Linguinou, « Pitchoune » (source)
11. Xavier Dandoy, « Recherches typographiques » (source)
12. Bruno Bernard, « Munegascu, une typographie pour écrire la langue monégasque », 23/11/2024 (source)
13. compart.com, « Unicode Character “Ꝃ” (U+A742) » & « Unicode Character “ꝃ” (U+A743) », (source & source)

Il y a quelques semaines maintenant sortait le 30e numéro de Graphisme en France — revue annuelle publiée par le CNAP — mise en forme cette année par Louise Garric, et utilisant le caractère Pachinko d’Émilie Rigaud de A is for fonts.

Le caractère tire à priori son origine du travail de thèse (sur le point de se conclure) d’Émilie sur l’histoire de la typographie japonaise. En forme d’hommage à la culture nippone, il intègre des formes de caractères encadrés, rappelant les machines-jeu d’où sortent des boules contenant des prix. Le terme pachinko étant d’ailleurs emprunté au nom de machines de jeu japonaises typiques.
Dans le GeF, ces formes encadrées sont en particulier utilisées pour les légendes des images et les notes. C’est sur ce point que nous reviendrons.

11 ou 1 et 1 ?

En effet durant ma lecture j’ai été quelque peu arrêté par les appels de notes dont le nombre dépassait 9. Dans un tel cas en effet, l’appel est constitué de deux glyphes encadrés et juxtaposés. Si la chose parait assez banale, cette coupure entre les deux chiffres m’a fait plusieurs fois douter de la façon donc je devais les lire : j’avais tendance à lire séparément le premier chiffre avant de réaliser qu’il devait être associé au second. Il ne fallait pas lire le [1][1] « 1 et 1 », mais bien « 11 ».

Évidemment je m’y suis habitué, mais il n’empêche que cela a soulevé une petite réflexion sur des moyens de gérer d’une meilleure façon l’utilisation de ces glyphes pour les combinaisons de chiffres.

Le cas Ceremony

J’ai ainsi repensé au cas de caractère Ceremony, du Studio Joost Grootens, distribué par la fonderie Optimo. Le caractère, dédié initialement à la création de cartes et à la data-visualisation, intègre une pléthore de glyphes encadrés (dans des cercles, des carrés, et toutes sortes de polygones), aussi il m’a paru intéressant de voir comment il gérait la chose.
Et effectivement, le caractère va un peu plus loin en utilisant la fonctionnalité OpenType contextual alternates (calt), qui permet de substituer les doublons de chiffres comme [1]‍[1] par une forme [11], intégrant donc dans un même bloc les deux composants, ce qui me parait bien plus clair à la lecture.

Néanmoins je trouvais alors une nouvelle limite : au-delà de 99, la fusion des chiffres saute. Si l’on avait souhaité avoir par exemple [111], on a en fin de compte [11]‍[1]. Le problème ne se pose pas systématiquement à priori, mais il n’est pas non plus improbable d’avoir besoin de nombres encadrés supérieurs à 99, comment faire donc ?

Emprunter à l’écriture de l’arabe

Pour rappel, l’écriture des langues arabe, en plus d’aller de droite à gauche, a une particularité qui pourrait être très intéressante : les lettres ont des formes qui varient selon leur place dans le mot, qu’elles soient en début, au milieu ou en fin de celui-ci. Pour chaque lettre de cet alphabet (plus précisément de cet abjad), il y a donc possiblement 4 formes : isolée, initiale, médiale et finale. Ce besoin est évidemment intégré dans les fonctions OpenType dédiées, et permet aux locuteurs d’écrire de façon fluide les langues l’utilisant.

Si l’on imagine transposer cette fonction de positionnement, on pourrait relativement facilement dessiner des glyphes permettant de créer des combinaisons sans limitation de taille, puisqu’OpenType s’occupera d’afficher les bonnes formes. Sans grand effort, on pourra avoir [1], [11], [111], etc.

Mettre les mains dans la pâte

Je m’y suis donc essayé, en me limitant à un seul glyphe (le 2) et en prenant comme point de départ le caractère Hanken Grotesk, et les résultats sont plutôt satisfaisants. À noter que cela se base sur l’interface de test de mon logiciel de création typographique (Glyphs), et pas en conditions réelles dans un éditeur de texte par exemple.

Les fonctions init, medi et fina, fonctionnent bien sur mon aperçu, et par acquit de conscience, j’ai également testé une version plus complexe de calt, qui reprend grosso modo l’idée des init-medi-fina, qui marche là aussi plutôt bien.

Voici ce que cela donne en termes de code de fonctions dans le logiciel, on remarquera la simplicité du premier test, et la plus grande lourdeur du second :

# Pour init + medi + fina (ici regroupés mais normalement séparés en trois) :  
sub two by two.init;
sub two by two.medi;  
sub two by two.fina;  ​  

# Pour calt :  
@initial = [space];  
@final = [space period comma];  
@letter = [two two.deb two.mil two.fin];  ​  

@initForms = [two.deb];  
@mediForms = [two.mil];  
@finaForms = [two.fin];      ​  

sub @initial @letter' @letter by @initForms;  
sub @letter @letter' @letter by @mediForms;  
sub @letter @letter' by @finaForms;

Il y a toutefois un souci sur ce second essai : quand je suis en début de ligne, le remplacement de la forme isolée par la forme initiale n’est pas opéré, et en essayant de corriger la chose je crée de nouveaux problèmes. Je suis assez peu expert, et j’imagine qu’il existe un moyen de pallier ce problème simplement, mais au moins par ces deux essais je pense pouvoir montrer que la chose est faisable, et finalement assez aisée dans la mise en place de base. L’application à de nombreux glyphes peut néanmoins alourdir le travail car à priori il faut définir les glyphes à la main et générer le code pour les calt à la main également, là où pour init, medi et fina, le logiciel s’en charge très gracieusement pour vous.
Il n’y a plus qu’à, comme on dit.

1. Graphisme en France, n° 30, CNAP, 2024 (source)
2. Pachinko (caractère typographique), Émilie Rigaud, A is For, 2020 (source)
3. Ceremony (caractère typographique), Studio Joost Grootens, Optimo, 2015 (source)
4. « Alphabet arabe », Wikipedia (source)

En 1876 Cesare Lombroso publie L’homme criminel, ouvrage défendant notamment la thèse que la criminalité est une caractéristique transmise de façon héréditaire, et dont on peut trouver des marques par l’étude physique des personnes. Avec une méthodologie que l’on pourrait qualifier de scientifique, il déploie ses arguments par de nombreuses études physiques et par l’adjonction de planches richement illustrées d’éléments prélevés dans la culture criminelle.

Les signes des marges

Si les planches sont légendées de façon assez précise sur le contexte et le sens des éléments, sur la planche XXXIV, la figure 5 est simplement nommée « Alphabet chryptographique des filous » (avec cette graphie spécifique) sans plus d’explication de son origine et de son usage. L’alphabet partiel représenté donne les correspondances entre les signes des filous et l’alphabet usuel. Un déchiffrage sans doute utile aux services de police de l’époque.

Du point de vue formel, les signes présentés sont basés sur des figures simples (lignes, cercle, coins, pointes) qui se combinent de façon séquencée : les formes en pointes se suivent (g à p), tout comme les coins (q à x). C’est une construction assez arbitraire, mais qui a le mérite de la simplicité et de l’économie de moyen.

Juste en dessous de l’alphabet se trouve une copie d’une inscription présentant à sa droite le dessin de deux sabres croisés qui, d’après la légende fournie, signifie le vol.

Ces fameux filous du XIX^e siècle possédaient donc un système de communication complet, un code, qui permettait à la fois de mettre en exergue leur particularité sociale, de souder leur communauté, et en même temps de permettre l’exclusion des autres groupes sociaux et dans le cas qui nous intéresse de rendre plus complexe le travail de la maréchaussée.

Dans un registre similaire comment ne pas penser au hobo code, un système de marques utilisé notamment par la communauté des travailleurs migrants états-uniens des XIX^e et XX^e siècles qui permettait, tel un système de signalisation routière, d’indiquer (entre autres) les lieux qui étaient à éviter et les lieux qui leur seraient favorables. Notons cependant que l’usage réel de ce code prête à débat et que des sources objectives manquent, de plus simples graffitis étant quant à eux attestés.

Si nous parlons surtout ici de lexiques visuels, il existe également un lexique partiellement cryptique pour l’oral ou l’écrit des filous. Le terme argot, dans son sens originel, désigne ce vocabulaire spécifique. Certains mots prennent un sens secondaire, d’autres sont inventés pour l’occasion afin de brouiller les pistes et assurer une certaine confidentialité des affaires pour le moins douteuses. Pour pousser cette question plus loin, je conseille la lecture de L’Argot de Pierre Guiraud (PUF, 1985), qui, bien qu’assez ancien, permet de se rendre compte de façon assez synthétique de la créativité linguistique de la petite délinquance française d’autrefois, qui n’a soit dit en passant rien à envier au lexique marketing de la startup nation d’aujourd’hui.

Hérédité, bosses du crâne et criminologie

Pour finir, revenons tout de même au travail de Lombroso. Si la présentation se veut scientifique, la qualité du travail a été remise en question dès sa publication et battu en brèche en particulier pour sa méthodologie bancale. La conception de l’hérédité des caractéristiques criminelle a amené à de nombreux abus et raccourcis. La phrénologie, pseudoscience, se proposait, par l’étude des bosses du crâne, de déduire le comportement de la personne, ses qualités comme ses tares. Mêlé au système d’anthropométrie judiciaire de Bertillon et la physiognomonie défendue par Lombroso, on en arrive rapidement à un mélange certes creux mais favorisant l’essentialisation des personnes, les théories racistes, antisémites (pensez au nez crochu des juifs par exemple), homophobes, et j’en passe. Un véritable racisme pseudoscientifique qui permet d’éclairer sous un jour nouveau les éléments ayant amené aux évènements mondiaux du XX^e siècle.

Si la chose parait absurde de nos jours, on en retrouve de forts stigmates dans les années 50 et 60, au sujet notamment de l’affaire Dominici, qui avait été un sujet de travail dans le cadre de mon DNA. Une émission de France culture, datée de 2020, revient sur ce phénomène persistant et suggère même son retour en force, appuyé cette fois par les progrès de la génétique. Si la science invalide des théories fumeuses rapidement, force est de constater que l’emprise sur le corps social est plus difficile à maitriser.

1. L’homme criminel, Cesare Lombroso, (version de) 1887 (source)
2. L’homme criminel — Atlas (deuxième édition), Cesare Lombroso, 1888 (source, pdf)
3. « Cesare Lombroso », Wikipedia (source)
4. « Physiognomonie », Wikipedia (source)
5. « Le retour de la théorie du ‹ criminel-né › », esprit de justice, France Culture, 02/12/2020 (source)
6. « Hobo », Wikipedia (source)
7. The mostly true story hobo graffiti, Vox, 16/07/2018 (source)
8. « Hobo signs, langage secret des vagabonds d’Amérique », Graphéine, 03/04/2023 (source)

J’écoutais il y a quelque temps un fameux streamer sur Twitch qui s’apprêtait à lancer un nouveau jeu en live qu’on lui avait très chaudement recommandé : Chants of Sennaar. Lui ayant été vendu comme un jeu d’enquête sur des langues à la DA magnifique qui n’avait pas à rougir du très bon Return of the Obra Dinn, sa curiosité avait été évidemment piquée. Ayant également adoré Return of the Obra Dinn et grand amateur des systèmes typo-graphiques, j’ai donc mis en pause le stream afin de ressortir ma Switch qui trainait dans un tiroir pour l’acheter et y jouer au plus vite.

Note : à la demande des développeurs, je limiterai au maximum les images présentant les signes à déchiffrer et les éléments d’enquête. Un droit de regard sur le texte leur a été accordé afin d’assurer qu’un minimum des éléments clefs soient montrés.

La tour de Babel comme aire de jeu

Dans Chants of Sennaar le joueur incarne un personnage qui doit progresser dans une gigantesque tour, métaphore assumée de la tour de Babel. Dans les cinq étages de celle-ci vivent cinq peuples aux cultures différentes : dévots, guerriers, bardes, alchimistes et reclus. Chacun de ces peuples possède une ambiance visuelle, une architecture et une pseudo-langue propre à découvrir.

Armé d’un simple carnet de notes (associant un signe de la langue rencontrée et une illustration) et de ses talents de déductions, le joueur doit donc tenter de déchiffrer la langue de chaque étage afin de résoudre des énigmes et de progresser dans le jeu. Quand l’ensemble des déductions d’une page sont correctes (association entre illustration et signe de la langue donc), les termes sont « validés » et on obtient la traduction officielle des termes rencontrés. Un système simple, mais efficace, où une compréhension partielle des mots permet tout de même d’avancer. L’idée n’est pas de trouver une traduction forcément exacte, mais de pouvoir comprendre l’idée sémantique du signe à déchiffrer, clef pour résoudre les énigmes et faire les bonnes actions dans le jeu.

Les environnements sont épurés, l’accent étant mis sur l’aspect visuel associé à chaque peuple. La caméra assez éloignée et bien souvent fixe permet de toujours profiter de l’espace dans lequel on déambule, on se croit parfois dans un tableau. Si l’inspiration n’est à priori pas revendiquée, j’y vois un parallèle de fond avec les propositions de Monument Valley ou encore de Journey.

Des signes inspirés par la culture écrite du monde

De l’aveu même des deux développeurs à l’origine du projet — Julien Moya et Thomas Panuel — les signes rencontrés n’ont pas été pensés pour créer de véritables langues, mais seulement un ensemble d’éléments de vocabulaire servant le gameplay. Par contre chaque peuple devant avoir un style propre, des inspirations ont été prises du côté de systèmes visuels réels.

Ainsi on peut retrouver pour certains peuples des références plus ou moins claires. L’alphabet phénicien, assez géométrique, ou le protosinaïtique pourraient être associés aux dévots. L’arabe et le devanagari collent plutôt aux bardes. L’alphabet runique aux guerriers. Dans le cas des alchimistes, on est plus face à des signes évoquant clairement la tradition des signes alchimiques, assez complexes, et formant presque plus des sortes de logos que des lettres. À mon sens, c’est le système des reclus qui est le plus éloigné des systèmes de signes connus, en m’évoquant plutôt des expérimentations graphiques plus contemporaines. Je ne peux m’empêcher de faire ici un parallèle avec certains des signes vus dans Letterform variations de Nigel Cottier.

Certains glyphes ayant un point commun sémantiquement parlant présentent également des similitudes graphiques. Des termes associés à des lieux ou aux noms des peuples auront donc des structures ou des parties similaires. Sur ce point les projets de pasigraphies, telles le Bliss ou le LoCoS usent de cette technique : cela permet d’apprendre et de comprendre plus aisément la logique de la langue, et pour le jeu, cela permet de guider de façon subtile l’avancée du joueur et de rationaliser le processus de design, tout le monde est content.

Jouer à ce jeu, c’est indirectement s’ouvrir à une culture visuelle très riche, mais parfois peu connue du grand public et qui représente le patrimoine graphique du monde et des peuples qui y vivent ou qui y ont vécu. Un bon message porté et assumé par le jeu, alors jouez-y.

1. Chants of Sennaar, Rundisc, Focus Entertainment, 2023 (source)
2. Chants of Sennaar, Focus Entertainment (source)
3. « Godot & la création de Chants of Sennaar », Atomium & Mister MV, Rencontre en terre indé, 03/10/2023 (source YouTube)
4. « Chants of Sennaar », Wikipedia (source)

À propos de l’auteur

Walter Bohatsch est un designer graphique et typographe autrichien, membre de l’AGI. Il a été un temps enseignant en design et en typographie et est le fondateur du studio de design graphique Bohatsch und Partner. Il a gagné plusieurs prix, dont « Le plus beau livre d’Autriche » en 1990, 2004 et 2007.

Un ouvrage de présentation d’un système typographique

Quand on tape « Walter Bohatsch » sur Google images, on tombe rapidement sur le projet qui est sans doute le plus célèbre de cet auteur : les Typojis, et notamment l’édition qui est associée.

Cet ouvrage, d’un format assez généreux de 187 × 250 cm pour 240 pages, est à la fois un spécimen, une présentation et un cahier d’apprentissage d’un caractère typographique comprenant 30 nouveaux signes de ponctuation signifiant les émotions et nommé Typojis. L’ouvrage est entièrement bilingue allemand-anglais et se segmente en plusieurs blocs. Le premier étant dédié à une présentation générale du système, suivi par une série de textes par des auteurs invités. L’essentiel du livre est occupé par un bloc de présentation des 30 signes, toujours présentés de la même manière : une photographie issue de la culture mondiale (politique, culture, etc.), le signe en pleine page, une double page de phrases d’exemple sur fond bleu en page de gauche, et en rouge en page de droite. Vient ensuite une double page en forme de cahier d’exercice de traçage du signe à la manière d’un cahier d’écolier, on peut ainsi s’entrainer au traçage de ces nouveaux glyphes. On finit par un spécimen complet du caractère typographique Typojis sur une page, montrant à la fois les 30 signes et les caractères usuels. À noter que l’ensemble de l’ouvrage est composé avec le-dit caractère, qui en soit suffit en tant que spécimen des caractères alphabétiques qui sont autrement moins mis en avant par rapport aux 30 signes pour les émotions.

À propos des typojis

Les typojis (on fera ici usage de ce terme pour désigner les signes spécifiques du caractère) codent 30 sentiments et tons : Optimisme, Pessimisme, Euphémisme, Exagération, Sympathie, Antipathie, Enthousiasme, Scepticisme, Intégrité, Tolérance, Ignorance, Surprise, Déception, Solidarité, Rejet, Sagacité, Naïveté, Admiration, Ennui, Mépris, Curiosité, Autorité, Provocation, Séduction, Challenge, Aspiration, Modestie, Secret, Outrage, et Ironie. Leur construction est basée sur la construction des signes d’exclamation et d’interrogation, avec un point en bas et une forme plus ou moins courbe en chef.

Certain signes codant pour des émotions opposées sont dessinés en symétrie, verticale par exemple pour l’Enthousiasme et le Scepticisme ou horizontale pour le cas de l’Euphémisme et de l’Exagération. Dans cette symétrie le point souscrit n’est jamais impacté, seul la partie supérieure l’est. Aucun de ces signes ne semblent pas s’inspirer de formes existantes de signes de ponctuation pour les émotions ou de formes graphiques connues. C’est particulièrement prégnant pour le signe pour la séduction, qui aurait pu évoquer une sorte de cœur, ce qui aurait indiqué la thématique générale invoquée.

Si certains signes sont faciles à écrire, d’autres le sont beaucoup moins, le signe pour la Provocation et la Séduction étant selon moi les plus difficile à prendre en main. Je sais que la pratique de l’écriture manuscrite s’amenuise, mais je me serai attendu à des formes avec un tracé relativement simple. On est bien là sur de la typographie, dans son sens mécanique, et pas dans la calligraphie, dans son sens manuel. D’ailleurs le caractère Andersen, dont j’ai parlé dans le billet précédent, et qui a une thématique similaire, n’est lui aussi pas adapté selon moi à un traçage manuel de ses signes. Dans les deux cas, on est là dans une proposition graphique pensée pour la composition de texte et sa lecture, pas pour son traçage.

Pour ce qui est de l’utilisation de ces 30 signes, c’est un simple système OpenType de ligature qui permet de les ajouter à un texte. Il suffit d’entourer le nom (anglais) du signe par les signes d’addition pour faire remplacer la formule par le signe correspondant. Par exemple pour l’Optimisme, on notera « +optimism+ ». Simple et efficace.

À propos du nom

Le terme « typoji » contraction assez claire de « typographie » et d’« emoji » évoque donc un système graphique bien connu de représentation d’émotions (bien que maintenant les emojis soient bien plus variés) sous forme de petites images. C’est là donc que je trouve que le nom donné, bien que je le comprenne, ne me semble pas le plus adapté. En effet l’intérêt des emojis réside dans leur forme illustrative, permettant, en théorie, une compréhension immédiate, ne nécessitant pas d’apprentissage particulier (c’est évidemment bien plus compliqué que cela) et donc adaptée à leur usage dans les conversations à l’heure d’internet et des réseaux sociaux. Ce sont des icônes. Selon moi, les typojis sont eux des signes à plus rapprocher du système de ponctuation, nécessitant donc un apprentissage de leur signification. Ce sont donc des symboles.

Disant cela, je ne résous pas le problème et il est clair que d’avoir choisi typoji connecte ce travail à une certaine contemporanéité en proposant des signes plus ‘typographiques’ et possiblement moins perturbant que les emojis, qui sommes toute ne sont quasiment pas utilisés dans la composition de textes littéraires par exemple, probablement car considérés comme trop familiers. Ce terme permet également d’inférer l’utilité et le domaine d’intervention de ce système. En cela le mot-valise typoji est tout à fait adapté. À vous maintenant de vous faire votre avis.

1. Typojis – A Few More Glyphs, Walter Bohatsch, Verlag Hermann Schmidt, 2017 (source)
2. Typojis – A few more glyphs, site web (source)
3. Bohatsch und Partner, studio de design (source)
4. “ Walter Bohatsch ”, wikipedia, (source)